October 2020 - Challenge
This month's challenge is dedicated to the memory of Frances Allen, who passed away in August. Among her many accomplishments is the invention of the control-flow graph, in her 1970 paper "Control flow analysis"
The control-flow graph of a program contains a node for each code block that has exactly one entry and one exit point (i.e., there are no jump commands inside the block) and an edge A -> B that indicates a possible transition from the last line of A to the first line of B (due to a jump command or simply B being placed right after A).
- We introduce a toy programming "language" with the following limited set of commands:
- "X = Y" where X and Y are either strings indicating variable names, or literal integers.
- "X = Y OP Z" where X, Y, Z are either strings or literal integers, and "OP" belongs to the set {+, -, *, /, %} with the usual meaning for this operations.
- "JMP A" where A is an integer, meaning the program jumps to the line denoted by A.
- "JMP_ZERO X A" where X is a string indicating a variable, and the program jumps to A only if X is 0.
- "RETURN X" which should be **the last line** in the program, denoting its return value.
- "CHAOS LINES" which indicates a random jump to one of the lines in LINES, which is a comma-separated list of integers.
A program consists of a sequence of lines, each containing a line number followed by an instruction.
Your goal: Find a program with at most **20** lines that starts with10 A = a 20 B = b
Where "a" and "b" are integers such that a > b, and that returns the greatest common divisor of a and b (for any a, b), such that in the program's control-flow graph, the number of paths from the entry node to the exit node of length $n$ is the sequence
0, 2, 2, 5, 8, 17, 32, 65, 128, 257,...
A bonus '*' for finding another program returning the greatest common divisor, such that the sequence of the number of paths from the entry to the exit node contains the number "1970" after at most 20 elements.
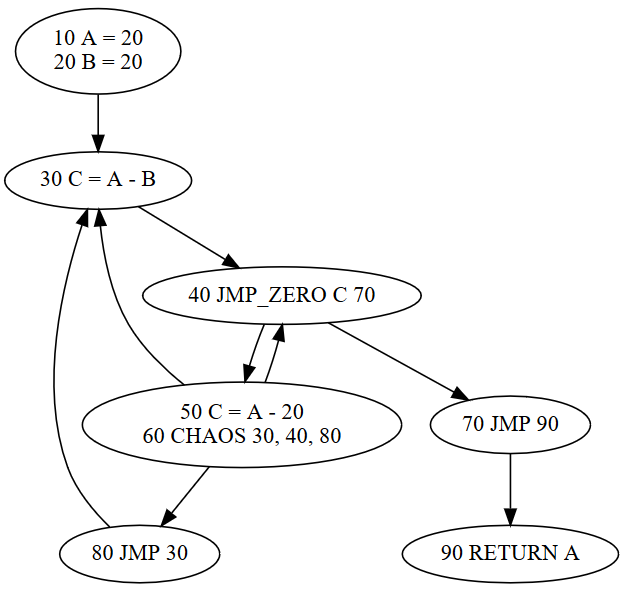
Here's a sample program, along with its control-flow graph:
10 A = 20 20 B = 20 30 C = A - B 40 JMP_ZERO C 70 50 C = A - 20 60 CHAOS 30, 40, 80 70 JMP 90 80 JMP 30 90 RETURN A
We will post the names of those who submit a correct, original solution! If you don't want your name posted then please include such a statement in your submission!
We invite visitors to our website to submit an elegant solution. Send your submission to the ponder@il.ibm.com.
If you have any problems you think we might enjoy, please send them in. All replies should be sent to: ponder@il.ibm.com
Challenge:
30/09/2020 @ 12:00 PM EST
Solution:
03/11/2020 @ 12:00 PM EST
List Updated:
12/09/2024 @ 11:30 AM EST
People who answered correctly:
Jacob Burnim(2/10/2020 6:53 PM IDT)
*Eden Saig(3/10/2020 3:24 AM IDT)
*Alper Halbutogullari(5/10/2020 5:54 AM IDT)
*Vladimir Volevich(6/10/2020 10:58 AM IDT)
Lorenz Reichel(10/10/2020 12:25 AM IDT)
*Florian Fischer(10/10/2020 11:20 PM IDT)
*David Greer(11/10/2020 12:01 AM IDT)
*Bert Dobbelaere(11/10/2020 9:56 PM IDT)
*Victor Chang(12/10/2020 8:34 PM IDT)
*Oscar Volpatti(14/10/2020 11:29 AM IDT)
*Latchezar Christov(14/10/2020 4:04 PM IDT)
*Dieter Beckerle(14/10/2020 11:42 PM IDT)
*Bertram Felgenhauer(16/10/2020 6:42 AM IDT)
Clive Tong(16/10/2020 8:56 PM IDT)
Kai Guttmann(24/10/2020 10:54 PM IDT)
Shouky Dan & Tamir Ganor(27/10/2020 8:36 AM IDT)
*Daniel Chong Jyh Tar(29/10/2020 4:22 AM IDT)
*Dan Dima(29/10/2020 10:45 AM IDT)
Uoti Urpala(30/10/2020 12:27 AM IDT)
Erik Wünstel(30/10/2020 12:29 AM IDT)
*Chris Shannon(31/10/2020 12:10 AM IDT)
*Motty Porat(31/10/2020 2:23 AM IDT)
*Kang Jin Cho(31/10/2020 7:19 PM IDT)
Daniel Bitin(31/10/2020 11:33 PM IDT)
Radu-Alexandru Todor(2/11/2020 2:54 AM IDT)
James Muir(2/11/2020 7:29 AM IDT)
*Li Li(3/11/2020 7:37 AM IDT)