Ponder This

Bragging:
The puzzle took me about 15 minutes to solve, and about two hours to lay out the solution in a coherent (I hope) manner. It isn't a world-shaking accomplishment, but these kind of puzzles usually frustrate me no end. I figured it would take days just to get the solution. So I've got a big head right now.

My solution:
My reasoning went as follows:

1. Fact: There are 8 total people at the party.
2. The maximum number of other people anyone can shake hands with is 6. Eight minus two (can't shake with yourself or your spouse).
3. Everyone at the party shook hands with a different amount of people! This seems to lead to a contradiction. If nobody could press the flesh with more than 6 people, then how could 8 folks each shake hands with a different amount of people?

BUT...someone might have shaken hands with no one at all. Antisocial, yes, but still a possibility.

AND...not all 8 people must have a different number. According to the instructions, I ask everyone else how many friends they shook with, and everyone else replies with a different number. One of their numbers could be the same as mine. One repeat (and only one) is therefore allowed.

These two nuances allow all the 7 possible handshake counts (6, 5, 4, 3, 2, 1, and 0) to be allocated to the 7 guests other than myself. Of course, at this point, we have no idea which number is the same as mine, but if you study probability, you can probably guess.

OK, enough text. Let's draw a picture. It's an artist's rendition of 8 people at a party, each one next to his or her spouse.



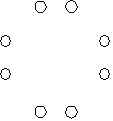
Now, Let's start with a person at random, call him Socialite Bob. Socialite Bob shakes hands with everyone except his spouse (So his total is 6 handshakes with different people).



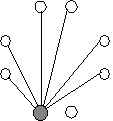
This gives everyone but Socialite Bob's spouse a handshake total of at least one, and Socialite Bob's spouse a handshake total of zero. We'll name her Antisocial Annie.

We also know that no two guests can both have a handshake count of 6 or 0. (6 and 0 cannot be the repeating totals) If more than one person has zero handshakes, Socialite bob cannot have six. And if more than one person has six handshakes, Antisocial Annie cannot have zero.



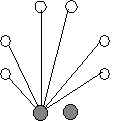
So...two down, six to go.

One of the remaining guests must have five handshakes. Since everyone but Bob and Annie has exactly one handshake so far, we can pick someone at random. Call her Friendly Jill.



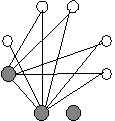
Three down, five to go.

OK, let's see. Friendly Jill shakes hands with everyone but her spouse and Antisocial Annie. That gives her the required handshake count of 5.

And, hey! Everyone except Friendly Jill's spouse has a handshake count of two. That must mean that Friendly Jill's spouse gets the handshake total of one. We'll call him Bad-Breath Ernie.



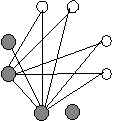
Four down, four to go.

Now, we pick one of the four remaining people and add two more handshake lines, bringing that person's total to four. Of course, we can't interfere with our previous selections, and we can't draw the lines to a person's spouse, so we have to do it like this. We'll call this person Four-Shake Fred.



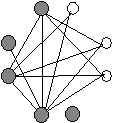
Five down...

It looks like Four-Shake Fred's spouse is two-shake Tammy.



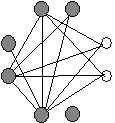
Six down...

Now, we take the remaining two, and...wait...Whoa! We're done!

Here are the handshake totals:



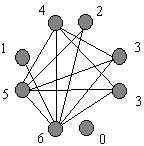
Hmmm... Each couple's total adds up to six. Weird.

So...Three is the repeating number! So one of those threes must be me, and one must be my spouse. But which ones? And who are Pat and Chris? (Forget those other goofy names. They were just for fun.)

Well, neither of those questions really matter because both people with three handshakes got those three handshakes from the exact same three people! And each of those three people was from a different couple! According to the instructions, one of those couples was Pat and Chris. We both definitely shook hands with Pat, and completely ignored poor Chris.

Conclusion:
This was a fun puzzle! I enjoyed the following things about it.

1. Without a detailed look at the instructions, the puzzle would have been impossible.
2. The puzzle did not require intense knowledge of probability theory.
3. The "real" puzzle did not lie in developing a correct mathematical formula to deal with the situation, but in developing a correct process by which to arrive at a solution.

download this solution in rich text (.rtf) format
My homepage