April 2014
The bottom line answer for the expected value of the maximum number in the array is, for N=5, 937669227/67108864 (which is approximately 13.97).
Kudus to Christopher Marks who was the first to solve this month's challenge without using programming at all, but rather by merely doing a careful examination of cases.
Among others, we also received the following solutions:
A one-line Mathematica solution from Todd Will:
ave[x_]:=ave[x]=If[Length[x]==5,Max[x],Mean[ave[Prepend[x,#]//.{a_,a_,b___}:>{2a,b}]&/@{2,4}]]
A small Haskel program from John Tromp:
import Data.Ratio
avg :: [Integer] -> Ratio Integer
avg ps | length ps >= 5 = maximum ps % 1
avg ps = (avg' (2:ps) + avg' (4:ps)) / 2
avg' :: [Integer] -> Ratio Integer
avg' = avg . reduce
reduce :: [Integer] -> [Integer]
reduce (a:b:ps) | a == b = reduce (a+b : ps)
reduce ps = ps
main = print $ avg []
And a PARI-GP program from Claus Andersen and David Brink.
Replace(v)=
{
if(#v<2,return(v));
if(v[#v-1]<>v[#v],return(v));
Replace(vector(#v-1,i,if(i<#v-1,v[i],v[i]+v[i+1])))
}
Next()=
{
if(t==0,return());
if(e[t]==2,
e[t]=4;L[t]=Replace(concat(if(t>1,L[t-1],[]),4)),
t--;Next())
}
April(n)=
{
p=0;
e=[2];
L=[[2]];
t=1;
s=0;c=0;j=0;
while(t>0,
if(#L[t]==n,
\\print(L[t]" "vector(t,i,e[i]));
j++;p+=vecmax(L[t])/2^t;Next(),
t++;
if(#e<t,e=concat(e,0));e[t]=2;
if(#L<t,L=concat(L,0));L[t]=Replace(concat(L[t-1],2))
);
);
return(p)
}
April(1)
April(2)
April(3)
April(4)
April(5)
John Snyder sent us a very detailed analysis of the problem. We chose to share his nice graphic representation of the Markov process here:
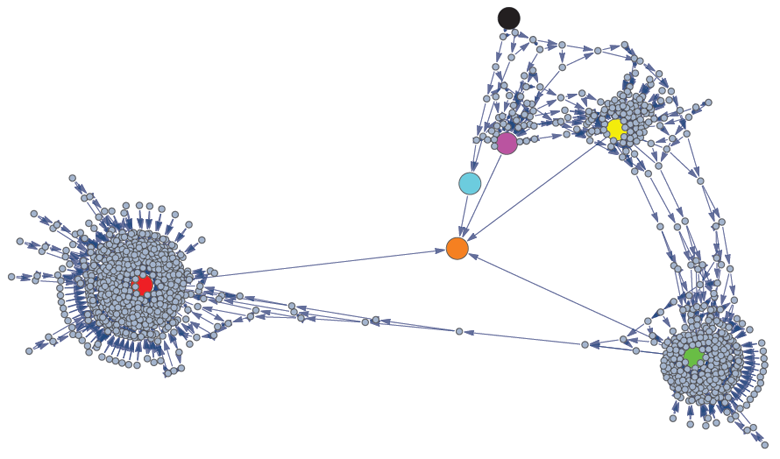
Graphic representation of the Markov process by John Snyder
Oleg Vlasii computed the answer for N=1,2,...,10 and noted the pattern
A(n) = (F(n)*2^(f(n)-1)+3^f(n))/2^(2^N-N-1)
where f(n) = 2^(n-1)-1
and F(n) are integers; but a closed form formula still eludes us.
If you have any problems you think we might enjoy, please send them in. All replies should be sent to: ponder@il.ibm.com